なぜかJOI予選通過しました。 ABCD4完で400点でした。D問題を通せなかったら当然落ちていたので、だいぶ危ない橋だったと思ってます。
DをACした流れがそこそこ壮絶(大袈裟な表現)だったので、ネタとして面白いかと思い記録に残そうと思います。ついでに予選体験記も書きます。
免責事項
この記事に書かれているDの解法はとても迂遠です。本当は座標圧縮も遅延セグ木も、なんなら累積和すら必要ありません。めっちゃシンプルな解法が存在します。
競プロのレートが上がるというのは、単に難しい問題が解けるようになるということだけじゃなくて、無駄な遠回りをしないようになるということなんですよ。知らんけど。
予選前
やる気がなかったので一切精進をしなかった。6月16日のABC100以来約6ヶ月ぶりの競プロで、本番前に問題を解いたりすらしなかったので完全に舐めプだった。
ちなみに、12時まで某進という塾で現代文の授業を受けてました。帰宅しておにぎり食べてパソコンに向かって準備してたら一瞬で開始時刻になった。ぶっちゃけ休みたかった
A問題
普通にループで回せばいいのに、算数的なO(1)解法を書いたらWAだった。
言い訳をすると、初めは普通に解けると思ってたんです。ボーナスでやっと超えるコーナーケースの存在に気が付いていませんでした。
10分消費。コーディングが遅すぎますね。
B問題
普通にシミュレーションするだけ。14分消費。コーディングが遅すぎる。
コーディングだけじゃなくて数学とか化学とか物理の試験もめちゃくちゃ遅いので、恐らく共通の原因がある。単に慣れていないからだと思うし、努力量でカバーしないとどうにもならないのは分かってるんですけどね。
C問題
OXOXと並んでいるとこを数えるだけ。10分消費。この時点で34分が経過している。
D問題(15点解法)
とりあえず、高さの種類だけが問題であることが分かる。で、大昔にちらっと読んだ蟻本によれば、こういうときに座標圧縮というテクニックを使うといいらしい。
座標圧縮なんて人生で一度も書いたことがないので、とりあえず書き方をググる。
どうやら、シェルスクリプトでいうところのsort | uniqをすればいいらしい。その後はインデックス(これが圧縮後の値になる)と元々の値の対応をmapか何かで保持しておいて、入力データを対応する圧縮後の値に置き換えていく。C++だとstd::uniqueとstd::vector::eraseという関数があって、これをセットにすることでコマンドのuniqと同じようなことができるっぽい。
あと、圧縮するときに高さ0も追加するのを忘れないようにする。
あとは高さごとに島を数えて最大値を出力する。15点分の部分点をゲット。ここで48分消費、この時点で82分が経過。
D問題考察(そして遅延セグ木の登場)
考察しているうちに、山の頂上(関数でいうところの極大)と谷の最下部(関数でいうところの極小)だけ考えればいいということに気付きました。

実際には「山の斜面」は段々ですけど、段々だと考えても島の数(ここでは3つ)は変わりませんね?
さらに、海面が横切った数は島の数の2倍です。この図だと6回横切っていて3つ島があります。海面が高さ0だと2回(両端)通過してて島の数は1(両端の高さを0にするのを忘れないように)、海面が最高峰を超えると1回も横切らないので島の数は0になります。
そして、ちょっと変形するとこうなりますね?
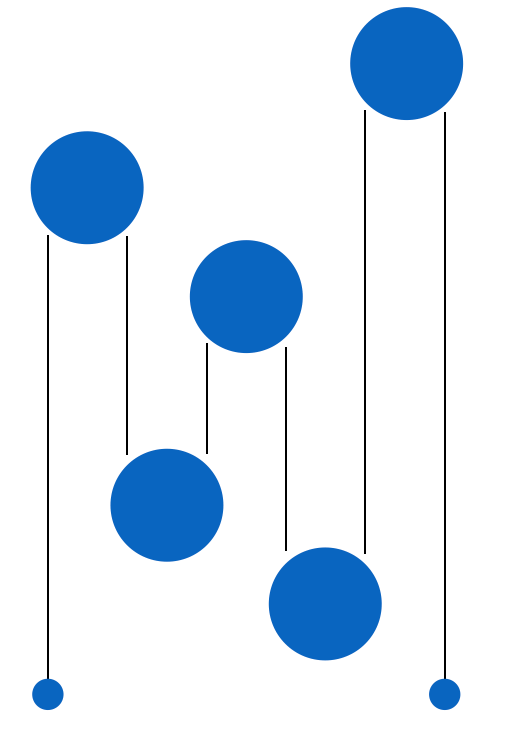
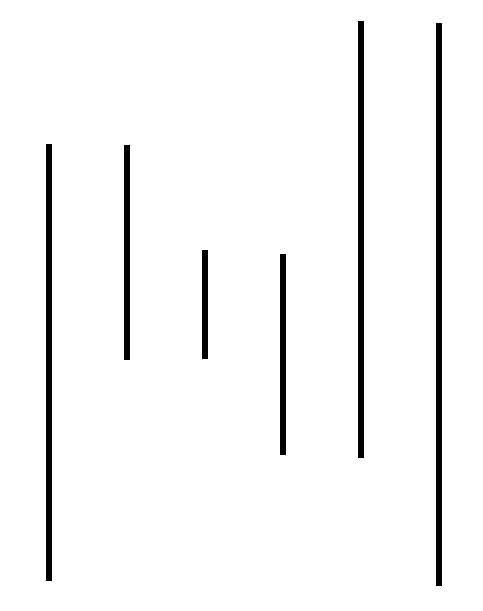
結局のところ、線分が最もたくさん重なっている部分を求める問題に帰着します。で、これって範囲加算を繰り返して最大値を取れば答えが出ますよね?

この場合だと、要素数6の配列を全部0で初期化して、
- 0から3までに全部1を足す
- 2から3までに全部1を足す
- 2から2までに全部1を足す
- 1から2までに全部1を足す
- 1から4までに全部1を足す
- 0から4までに全部1を足す
こうすると、配列の中身は2,4,6,4,2,0になります。配列の最大値は高さ2のときの6で、このとき島の数は3ですね。
注: 谷間が海面と同じ高さだと島が分かれるので通過2回、頂上が海面と同じ高さだと島ができないので通過0回とカウントしないといけません。つまり、線分の低い方の端を通過したらカウントし、高い方の端を通過したらカウントしません。だから1本目は0から4ではなく0から3まで足すのです。
でも、こんな足し算を普通にやっていると絶対にTLEします。じゃあどうしましょう?
データ構造で殴ればいいのです
遅延セグ木
ある列に対して連続する区間に対して更新(例えば加算)と取得ができるデータ構造です。なんかセグ木というデータ構造があって、その強い版らしい。
残念ながら、私の手元にはまともなライブラリがありません。Union Findすらありません。実装がめちゃくちゃ遅い人間なので、新しいデータ構造を実装すると絶対に間に合いません。理解するのも……私の頭では厳しい。天才なら一瞬で理解しそうですけど。
なんなら遅延セグ木を使うのも人生で初めてです。
どうせこういう有名な(少なくとも競プロでは)データ構造はライブラリが既にあるはずです。そう思って、いろんな競プロerがGitHubなどに上げている競プロ用ライブラリ(スニペット)を調べてみました。
しかし、どれもドキュメントがないんですね。そりゃ自分用ライブラリなので当然なんですけど。
万事休すかと思われたその時、私はとある記事を発見しました。
この記事が素晴らしいのは、実際にACしているコードのリンクを貼ってくれていることです。しかも、解いている問題がめちゃくちゃシンプル。クラス(C++だとクラスと構造体は同じ)とかメソッドの使い方を把握するにはうってつけでした。
実際、範囲指定は閉区間なのか半開区間なのかとか、0-indexedなのか1-indexedなのかとか、そういう細かいとこでハマらなくて済みました。
というわけで、遅延セグ木の部分をコピーして、 足し算を実装して、最終的な値を1つずつ取得して最大値を求めれば勝ちです。
76分消費してAC。この時点でだいたい160分経過していました。
E問題
bit全探索書こうとしたけど時間切れ。実装が遅い弊害がこんなところに。
教訓
遅延セグ木ってのは、ぶっちゃけAtCoder水色すら怪しいレベルの人(ふぁぼん)が使うもんじゃないです。遅延セグ木なんて知らなくてもレート1200くらいのレベルだったら全く問題ないです。マジで。
レベルが低いくせになまじデータ構造等の知識があると、素朴な解法を思い付かず実装等に無駄な時間を使うことになります。身の丈に合った道具を使いましょう。冷静に考えたら分かりますが、JOIのD問題に遅延セグ木なんて出てくるわけがないんですよ。
とはいえ、JOIは私みたいな実装が苦手なクソ雑魚プログラマには比較的向いていると思います。時間が3時間もあるし、調べ物だって許可されているので、初めて実装するアルゴリズムやデータ構造でもなんとかなる場合があります。
競プロ一切できないのに本選に行って案の定何もできずに100点取って帰ってきた前科が(2回も)ある私が言うので間違いないです。
というわけで、競技プログラミングができなくても(場合によっては)JOIの予選だけなら突破できることがあるという話でした。おしまいおしまい。
本当に?
ここまで読んで、「お前それアルゴリズムを思い付いた前提で話してるけどそこがまず無理やろ」ということに気が付いた人もいると思います。大正解です。
人によって得意な分野は様々なので、精進しないなら自分の得意なとこが出るように祈祷しとけばいいと思います。祈祷に頼るのが嫌なら精進しろ。悲しいけどこれが現実です。私は精進が面倒だったので祈祷しました。
私はDPが本当に解けなくて(精進してないので当然)、アドホックな感じの問題は比較的解ける傾向にあるようです。グラフは知らん。
だから、4問目ないし5問目でアドホックな問題が出たら予選通過できる可能性があるし、両方DPだったら絶対に落ちます。4年中3年も通ったのは運が強烈に良かったからとしか言いようがない。
追伸
区間に足し算をしていくが個々の値をみるのが少ない場合、累積和みたいな感じでやると簡単です
— だま(競プロ) (@dama_code) 2018年12月14日
ア
そういや2017年のフェーン現象、途中まで「これ遅延セグ木必要なのでは……?」と思ってました。でも考察の結果、隣との差を保持するだけで十分(要は累積和の要領)ということが分かったんです。詳しくは解説PDFを読んでください。
https://www.ioi-jp.org/joi/2016/2017-ho/2017-ho-t1-review.pdf
で、今回の問題も大して変わりません。こんなに似ているのに、解いている間は必死すぎて「これフェーン現象と似てるな?」ということすら頭にありませんでした。こんなんだからクソ雑魚なんですね。
今この瞬間、私は「前に解いた問題から学習するということができない最弱プログラマ」の称号を得ました。一生返上できない気がします。